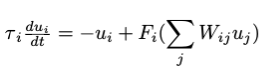Talk:Geometry

Resource repository

This section is to be used as a store for to-be-reviewed materials that may be incorporated as citations, external links, or literature section items.

Neurological Analysis

Patterns arise because of unstable spatially inhomogeneous perturbations in neurons through weakening cortical inhibition.

“The primary visual cortex, V1, represents external stimuli as patterns of neural excitation. In the normal state, patterns of excitation on V1 are driven by sensory stimuli generated in the retina mapped to V1 from the visual field by the retinocortical map (1, 2). Patterns seen as visual hallucinations arise in exceptional circumstances when external stimuli are overwhelmed by internally generated spontaneous patterns of neural excitation. This situation occurs when the circuit parameters governing the dynamics of V1 are changed, for example, through the influence of psychotropic drugs that may act in part through effectively weakening cortical inhibition (3)”

“Provided couplings that promote excitation, such as w_EE, are sufficiently large compared to relaxation and inhibitory couplings, Eq. Eq. 1 with lattice scale effects neglected (g^1_ij = 0), support a stable fixed point at nonzero excitation levels of both excitatory and inhibitory neurons. When such effects are restored, normal vision corresponds to a stable homogeneous steady state. Failure of normal vision to geometric visual hallucinations occurs when the homogeneous steady state becomes unstable to spatially inhomogeneous perturbations, leading to regular pattern formation (see Fig. 2A)“ [Figures and Equations are under copyright]

“Together, the results indicate that 5-HT2A receptor activation induces primarily by attenuating ongoing α oscillation a dysbalance between the excitability observed in the absence of an external stimulus and the excitability that is induced by the presentation of the stimulus. The dysbalance may reflect a shift away from external stimulus-driven toward internal-driven information processing and therefore may be a determining factor for the formation of visual hallucinations. In line with this view, several computational models postulate that an increase in the excitability of the visual network in the absence of visual input destabilizes spontaneous neuronal activity, which results in the formation of elementary visual hallucinations (Ermentrout and Cowan, 1979; Bressloff et al., 2002; Gutkin et al., 2003; Butler et al., 2012) that resemble the visual hallucinations produced by classic hallucinogens (Klüver, 1966; Siegel et al., 1975). In addition, increased stimulus-independent excitability that is associated with low α power values is implicated in TMS-induced phosphenes because the likelihood of experiencing these percepts is higher during low α power values relative to high α power values (Romei et al., 2008b). Psilocybin both strongly increased excitability in the absence of externally presented stimuli by decreasing α power values and robustly induced elementary hallucinations in almost all of the subjects. Together, these results suggest that these α effects may be involved in the formation of visual hallucinations. However, the correlation between the psilocybin-induced decrease in α power values and the subject-reported intensity of visual hallucinations did not reach statistical significance, indicating that the α power decrease induced by psilocybin may not be sufficient to generate a subjectively experienced visual hallucination.”

Broadband Cortical Desynchronization Underlies the Human Psychedelic State

Supposing instabilities arise due to neuronal excitations via hallucinogens, then it is possible that the background state (of your vision) can become unstable leading to a spontaneous pattern of activity reflecting the associative organization of the recurrent network (going to your brain).

p. 217 “Let us first consider a very general neural network architecture:

which represents the activities of many coupled neurons. W_ij represents the strength of connections between neurons so that Eq. (5) is a generalization of Eq. (4).This network can be separated into as many layers as desired; we include no intrinsic organization. Suppose that we subtract off the background activity of the network so that u_i(t) represents the deviation from background and F_i(0) = 0. For simplicity, we set τ_i = 1. We can ask whether or not this background state is stable.To determine this, we need to linearize about the rest state, u = 0. The stability is determined by the eigenvalues of the matrix:

M = -I + Q.

where Q_ij = F_i'(0)W_ij. If Q is small enough (that is, there is only weak coupling between units or F_i prime(0) is small) then the eigenvalues of M have negative real parts and any perturbations decay to the background state. However, suppose some external influence (e.g. flickering light, hallucinogens, etc) “excites” the network by, for example, making the slopes of F_i large. Then, it is possible that some eigenvalues of M can become positive and this leads to instabilities. The “shape” of the activities that arise from this instability is, to lowest order, a combination of all the eigenvectors of Q whose eigenvalues have simultaneously become positive. Generically for a random symmetric network, we expect either a transcritical or pitchfork bifurcation leading to a single excited mode reflecting the organization of the random network. If the effect of hallucinogens or other external stimuli is to produce an overall increase in excitability of the network, then is it possible that the background state can become unstable leading to a spontaneous pattern of activity reflecting the associative organization of the recurrent network. If there are many nearly identical eigenvalues, then the resulting patterns can be complex mixtures of the eigenvectors and the dynamics governing the patterns.”

p. 218 “This map coupled with the idea that visual hallucinations arise as a consequence of stability loss, first in striate cortex and later in higher association areas, allows us to explain the form constants of Kluver and indirectly explain the abstract designs of shamanistic paintings. Ermentrout and Cowan [3] exploited the symmetry of connections based on spatial position and used group theory to show that the spatial patterns which bifurcate from the background state are nothing more than stripes and spots.”

“Biologically informed modeling has suggested that instability within the primary visual cortex may facilitate the emergence of geometric hallucinations via self-organized patterns of neural excitation (30), and eyes-closed fMRI recordings during ayahuasca hallucinations suggest the visual cortex behaves “as if” there is external input when there is none (31) (see also ref. 29). The present findings of increased visual cortex CBF, expanded V1 RSFC, and decreased alpha power may be seen as consistent with the notion of “seeing with eyes-shut” under psychedelics, because they are all properties normally associated with visual stimulation (32, 33). Cortical alpha has been hypothesized to serve a general inhibitory function, filtering out “stimulus-irrelevant” information (34). Thus, reduced alpha power (9, 29, 35) could have disinhibitory consequences, facilitating the release of anarchic patterns of excitation that manifest spontaneously and experientially as visual hallucinations. This hypothesis is leant (indirect) support by two prior studies that found reduced spontaneous visual cortex alpha power under psilocybin alongside reduced evoked visual responses (9, 29). Further work, using higher-resolution brain imaging, machine learning techniques, dynamic measures of functional and effective connectivity, and improved “capture” of visual hallucinations (e.g., via button press or experience sampling), may help to develop this appealing model (e.g., see ref. 36).“

Due to the packing of the retinal cells we can predict the retino-cortical map for pattern emergence.

p. 299 “In the second part of this paper we study the nature of various even and odd combinations of eigen-functions or planforms, the symmetries of which are such that they remain invariant under the particular action of E(2) we have imposed. These symmetries correspond to certain subgroups of E(2), the so-called axial subgroups. Axial subgroups are important in that the equivariant branching of lemma indicates that when a symmetrical dynamical system becomes unstable, new solutions emerge which have symmetries corresponding to the axial subgroups of the underlying symmetry group. This is precisely the case studied in this paper. Thus we study the various planforms that emerge when our model V1 dynamics become unstable under the presumed action of hallucinogens or flickering lights”

p. 13 “Several theoretical explanations for geometric visual hallucinations have been proposed based on retinocortical mapping and the architecture of V1 [401,402,403,404,405]. According to these mathematical models, excitation of V1 neurons produces self-organizing patterns of activity that correspond to Klüver’s form constants. The excitation of V1 is presumably driven by 5-HT2A receptors because ketanserin blocks the visual hallucinations induced by psilocybin [85,89]. There are moderate to high densities of 5-HT2A receptors in V1 , with the highest level occurring in geniculorecipient sublayer IVc [350]. Similar to other cortical regions, almost all glutamatergic pyramidal neurons and very few GABAergic interneurons in V1 express 5-HT2A mRNA [407,408]. A recent electrophysiology study conducted in anesthetized macaque monkeys revealed that DOI produces a combination of excitatory and inhibitory effects in V1, exciting neurons with low firing rates and inhibiting neurons with high firing rates [407]. Since neuronal firing in V1 is driven by visual stimuli, one possible interpretation is that DOI reduces the response to visual input while enhancing spontaneous internally driven activity. It is fairly well-established that hallucinogens reduce retinocortical transmission [409,410,411]. Indeed, psilocybin inhibits N170 visually evoked potentials in human subjects via 5-HT2A [89,412]. Visual input stabilizes network activity in V1 by driving inhibitory interneurons [413]. Therefore, a reduction of visual input, coupled with an increase in the excitability of pyramidal neurons, could destabilize network activity in area V1, generating patterns of neuronal firing that are perceived as geometric form constants."

5-HT2A receptors are crucial for visual organization processes

p. 13 "The excitation of V1 is presumably driven by 5-HT2A receptors because ketanserin blocks the visual hallucinations induced by psilocybin [85,89]. "

“The decrease of N170 potentials by 5-HT2A receptor activation might be associated with visual perceptual distortions because N170 potentials are crucial for perceiving coherent and meaningful structures in natural images. Natural visual scenes often provide ambiguous and incomplete retinal information about objects; therefore, perceptual organization mechanisms are required for integrating local edge information into complex object representations and for interpolating missing parts of objects. These visual organization processes are associated with N170 potentials (Herrmann and Bosch, 2001; Murray et al., 2002), which are localized to the 5-HT2A receptor-rich LOC and V2 visual areas (Murray et al., 2002; Kometer et al., 2011; Savli et al., 2012). Thus, 5-HT2A receptor activation within the LOC and V2 visual area is likely to decrease N170 potentials, leading to incoherent object representation and arbitrary filling-in processes. On the other hand, the activation of 5-HT2A receptors decreases attentional resources (Kometer et al., 2012; Quednow et al., 2012), which are crucial for visual organization processes (Zhang and von der Heydt, 2010; Zaretskaya et al., 2013).”

It's implied that the site of geometry is cortical rather than retinal

p. 1638-1639 “Deep pressure on the eyeball does not seem to be the only way of evoking phosphene percepts of the regular grid type. Young. Cole. Gamble and Rayner. (1975) describe coarse honeycomb, fine honeycomb and rectangular grid patterns that can be elicited by viewing a uniform field flickering at appropriate rates. Furthermore, Welpe (1975) reports that a chessboard pattern observed in a uniform flickering held an be evoked only with binocular viewing of the flickering field. This was taken to imply that the site of occurrence was cortical rather than retinal. The geometric deep pressure patterns here show a similar limitation to binocular stimulation and are therefore probably also cortical.

I have argued that the monocular point arrays are not retinal in origin. since the deep pressure probably “pressure-blinds” all retinal function. It is tempting to opt for the lateral geniculate nucleus as the site, since it is the next synaptic junction beyond the retina. and also has punctate receptive fields. The lack of occurrence of point arrays with binocular deep pressure might result from reciprocal inhibition between the layers in the geniculate fed separately by the two eyes. Why the points should be so widely spaced is not evident. whether they arise in the retina, the geniculate or the cortex.“

The mechanisms to produce geometric hallucinations are conjectured to be closely related to those that process textures.

p. 473-474 “We model V1 as the continuum limit of a lattice of interconnected hy- percolumns, each comprising a number of interconnected iso-orientation columns. Based on anatomical evidence, we assume that the lateral connectivity between hypercolumns exhibits symmetries, rendering it in- variant under the action of the Euclidean group E(2), composed of reflections and translations in the plane, and a (novel) shift-twist action. Using this symmetry, we show that the various patterns of activity that spontaneously emerge when V1’s spatially uniform resting state becomes unstable correspond to the form constants when transformed to the vi- sual Želd using the retino-cortical map. The results are sensitive to the detailed specification of the lateral connectivity and suggest that the cortical mechanisms that generate geometric visual hallucinations are closely related to those used to process edges, contours, surfaces, and textures.”

Additional Papers

• Neural interactions between flicker-induced self-organized visual hallucinations and physical stimuli
• A mathematical theory of visual hallucination patterns.
• A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue
• The visual cortex as a crystal